Try the online demo here
Table of contents
What is Morphing Faces?
Morphing Faces is an interactive Python demo allowing to generate images of faces using a trained variational autoencoder and is a display of the capacity of this type of model to capture high-level, abstract concepts.
The program maps a point in 400-dimensional space to an image and displays it on screen. The point’s position is initialized at random, and its coordinates can be varied two dimensions at a time by hovering the mouse over the image, which produces smooth and plausible transitions between different lighting conditions, physical features and facial configurations.
Installation
Installation is as simple as downloading the code uncompressing it wherever you want. In addition to Python, Morphing Faces depends on the following Python packages:
Running the demo
In the morphing_faces directory, type
python visualize.py
You should see a matplotlib figure appearing. Now, hover the mouse over the picture and the face should transform.
The mouse’s relative position in the image is tied to the coordinates of two of the 400 dimensions: bottom-left corresponds to (-1, -1) and top-right corresponds to (1, 1).
What about other dimensions? 400 is quite a large number, and most of them don’t
do much (this a consequence of the training procedure), but the 29 most
interesting dimensions are available to try. Simply type d D1 D2 in the
command line interface, where D1 and D2 are two numbers between 0 and 28, in
order to select dimensions D1 and D2 to experiment with.
Maybe by now you found a way to create a funny facial expression and you would like to keep it that way while you play with other dimensions. In that case, click on the image to freeze it, change the selected dimensions and click the image again to unfreeze it. The coordinates in the two previous dimensions will be kept frozen, while you can interact with the newly selected dimensions.
If you’re bored with the current face and would like to see something else, type
r in the command line interface to pick another face at random. Behind the
scenes, a new point in the 400-dimensional space was chosen, and you can
move around it the usual way.
Finally, when you’ve had enough, simply type q in the command line interface
to quit.
How does it work?
This section supposes a background in probabilities and recapitulates basic concepts of probabilistic graphical models before introducing variational autoencoders. For a (much) more thorough treatment of probabilistic graphical models, see the excellent Probabilistic Graphical Models - Principles and Techniques textbook written by Daphne Koller and Nir Friedman.
Probabilistic graphical models and Bayesian networks
For the sake of simplicity, we will assume that all variables introduced in this section are discrete. Note that everything also applies for continuous variables if sums are replaced by integrals where appropriate.
A probabilistic graphical model is a way to encode a distribution over random variables as a graph, which can potentially yield a very compact representation compared to regular probability tables. It does so by encoding dependences between variables as edges between nodes.
Bayesian networks are a category of probabilistic graphical models whose graphical representations are directed acyclic graphs (DAGs). The probability distributions they encode are of the form
\[ P(X_1, X_2, \cdots, X_n) = \prod_{i=1}^n P(X_i \mid \mathcal{Pa}(X_i)) \]
where \( \mathcal{Pa}(X_i) \) is the set of \( X_i \)’s parents in the graph.
This concept is better illustrated by an example:
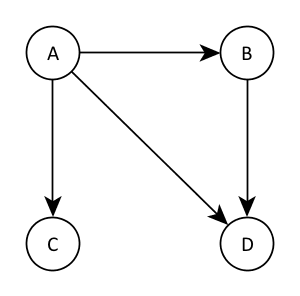
Here, \( A\) has no parents, \( B \)’s parent is \( A\), \( C \)’s parent is \( A\) and \( D \)’s parents are \( A \) and \( B \). The probability distribution encoded by this graph is therefore
\[ P(A, B, C, D) = P(A) P(B \mid A) P(C \mid A) P(D \mid A, B) \]
Learning bayesian networks, and the inference problem
Bayesian networks are interesting by themselves, but what’s even more interesting is that they can be used to learn something about the distribution of the random variables they model. Suppose you are given a set of observations \( \mathcal{D} \), and suppose that the conditional distributions required by your bayesian network are parametrized by some set of parameters \( \theta \). The act of learning the distribution which generated the observations could be described as follows: a parametrization of the model that approaches the true distribution is a parametrization under which observations in \( \mathcal{D} \) have a high probability, or alternatively, a high log-probability (because the logarithm is a monotonically increasing function). More formally, we are searching \( \theta^* \) such that
\[ \theta^* = \arg\max_\theta \log P(X_1, \cdots, X_n) = \arg\max_\theta \sum_{i=1}^n \log P(X_i \mid \mathcal{Pa}(X_i)) \]
This parameter search can be done by various ways, for instance by gradient descent.
This problem is straightforward if all variables are observed. Unfortunately, this is not always the case. Suppose that in the example presented earlier only \( C \) and \( D \) are observed, and the value of \( A \) and \( B \) is always unknown (we would say that the former are visible or observed variables, while the latter are hidden or latent variables). In that case, all we’re really interested in is to maximize the likelihood of \( C \) and \( D \) under the model, i.e. maximize
\[ P(C, D) = \sum_{A}\sum_{B} P(A, B, C, D) \]
Now things get hairy. What if \( A \) and \( B \) can take a great number of values? What if, instead of the toy example presented above, the bayesian network contains thousands of nodes, only a dozen of which are observed? The summation quickly becomes untractable, and this does not bode well: how can you maximize a quantity you cannot even evaluate?
One way out of this, which is oftentimes used in practice, is a technique known as expectation-maximization. Unfortunately, it assumes that the conditional distribution of the hidden variables given the observed ones is easy to compute, and this is not always the case. What can we do, then?
Variational autoencoders
Instead of seeking to maximize the likelihood, we could maximize a lower bound of the likelihood: if the lower bound increases to a given level, we’re guaranteed the likelihood is at least as high.
If your hidden variables are continuous, you can use one such lower bound, introduced by (Kingma and Welling, 2014) and (Rezende et al., 2014): variational autoencoders (VAEs).
Formal setup
Let \( \mathbf{x} \) be a random vector of \( D \) observed variables, which are either discrete or continuous. Let \( \mathbf{z} \) be a random vector of \( N \) latent variables, which are continuous. Let the relationships between \( \mathbf{x} \) and \( \mathbf{z} \) be described by the figure below:

The probability distribution encoded by this DAG has the form
\[ p_\theta(\mathbf{x}, \mathbf{z}) = p_\theta(\mathbf{z}) p_\theta(\mathbf{x} \mid \mathbf{z}) \]
where the \( \theta \) subscript indicates that \( p \) is parametrized by \( \theta \).
Furthermore, let \( q_\phi(\mathbf{z} \mid \mathbf{x}) \) be a recognition model whose goal is to approximate the true and intractable posterior distribution \( p_\theta(\mathbf{z} \mid \mathbf{x}) \).
The VAE criterion
In such a setting, the following expression is a lower-bound on the log-likelihood of \( \mathbf{x} \):
\[ \mathcal{L}(\mathbf{x}) = - D_{KL}(q_\phi(\mathbf{z} \mid \mathbf{x}) \mid\mid p_\theta(\mathbf{z})) + \mathrm{E}_{q_\phi(\mathbf{z} \mid \mathbf{x})} [\log p_\theta(\mathbf{x} \mid \mathbf{z})] \]
For a complete and very well-written derivation, see (Kingma and Welling, 2014).
We note that the expression contains two terms. The first term, which can sometimes be integrated analytically, encourages \( q_\phi(\mathbf{z} \mid \mathbf{x}) \) to be close to \( p_\theta(\mathbf{z}) \). The second term, which needs to be approximated by sampling from \( q_\phi(\mathbf{z} \mid \mathbf{x}) \), can be viewed as a form of reconstruction cost.
Without the first term, this model is simply an autoencoder. It can learn any perfectly invertible representation, including the identity, and nothing encourages it to learn a representation which is compatible with the prior distribution \(p_\theta(\mathbf{z}) \). The first term ensures that while training, the autoencoder learns a decoder that, at generation time, will be able to invert samples from the prior distribution such that they come from the right distribution, i.e. they look just like the training data.
The reparametrization trick
The most crucial detail about VAEs is called the reparametrization trick and deals with gradient propagation: since the reconstruction term is estimated by sampling, how can we propagate the gradient signal through the sampling process and through \( q_\phi(\mathbf{z} \mid \mathbf{x}) \)?
We do so by making \( \mathbf{z} \) be a deterministic function of \( \phi \) and some noise \( \mathbf{\epsilon} \):
\[ \mathbf{z} = f(\phi, \mathbf{\epsilon}) \]
such that \( \mathbf{z} \) has the right distribution. For instance, sampling from an isotropic normal distribution can be done like so:
\[ \mathbf{z} = \mu + \sigma \mathbf{\epsilon} \]
This is what allows VAEs to be trained properly: without the reparametrization trick, there is no efficient way of adapting \( q_\phi(\mathbf{z} \mid \mathbf{x}) \) to help improve the reconstruction.
A concrete example
Let the prior distribution on \( \mathbf{z} \) be an isotropic gaussian:
\[ p_\theta(\mathbf{z}) = \prod_{i=1}^N \mathcal{N}(z_i \mid 0, 1) \]
and let the approximate posterior distributions be normal and factorized:
\[ q_\phi(\mathbf{z} \mid \mathbf{x}) = \prod_{i=1}^N \mathcal{N}(z_i \mid \mu_i(\mathbf{x}), \sigma_i^2(\mathbf{x})) \]
Then the KL-divergence term integrates to
\[ D_{KL} = \frac{1}{2} \sum_{i=1}^N 1 + \log(\sigma_i^2(\mathbf{x})) - \mu_i^2(\mathbf{x}) - \sigma_i^2(\mathbf{x}) \]
Once again, a complete derivation of this result can be found in (Kingma and Welling, 2014).
Note that the functional form of parameters in \( \theta \) and \( \phi \) has not been specified yet. This means the encoding and decoding networks that output parameters can have any differentiable form you’d like.
Demo model
The model trained for this demonstration is exactly like the model described in the previous section and has the following properties:
- 400-dimensional latent space
- Encoding network has two hidden layers with 2000 rectified linear units each
- Decoding network has two hidden layers with 2000 rectified linear units each
- Isotropic gaussian prior distribution: \[ p(\mathbf{z}) = \prod_{i} \mathcal{N}(z_i \mid 0, 1) \]
- Isotropic gaussian approximate posterior distribution: \[ q(\mathbf{z} \mid \mathbf{x}) = \prod_{i} \mathcal{N}(z_i \mid \mu(\mathbf{x}), \sigma^2(\mathbf{x})) \]
- Isotropic gaussian conditional distribution: \[ p(\mathbf{x} \mid \mathbf{z}) = \prod_{i} \mathcal{N}(x_i \mid \mu(\mathbf{z}), \sigma^2(\mathbf{z})) \]
- Trained on the unlabel set of images of the Toronto Face Database